ФЕДОРІВСЬКИЙ ЦЕНТР ПО Міністерство освіти і науки України
Опрацювати відеоурок, записати основну теоретичну інформацію, приклади
Логарифмічними рівняннями називаються рівняння, що містять невідому величину під знаком логарифма або його основі (або в обох місцях одночасно). Їх легко звести до квадратних чи степеневих рівнянь відносно змінної, якщо знати властивості логарифма. Для прикладу, логарифмічними будуть наступні рівняння
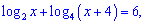
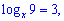
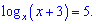
Необхідно відзначити, що під час розв’язку логарифмічних рівнянь необхідно враховувати область допустимих значень (ОДЗ): під знаком логарифма можуть знаходитись тільки додатні величини, в основі логарифмів – додатні, відмінні від одиниці. Проте знаходження ОДЗ деколи може бути дуже громіздким і на практиці маємо можливість вибрати: шукати ОДЗ або зробити перевірку коренів у рівняння.
Найпростішим логарифмічним рівнянням називають рівняння виду
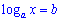
Його розв’язок обчислюється потенціюванням (знаходження числа або виразу за його логарифмом)
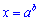
В деяких випадках, розв’язуючи логарифмічні рівняння, доцільно робити заміну змінної. Наприклад, у рівнянні
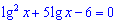
зручно зробити заміну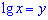 
і ми приходимо до квадратного рівняння. Причому обидва корені цього квадратного рівняння можна підставити в заміну, щоб знайти відповідне х.
Варто запам’ятати, що десятковий логарифм від одиниці з наступними нулями дорівнює кількості нулів у запису цього числа.
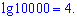
Для десяткового логарифма від виразів вигляду 0,00001 в правило подібне. Він рівний кількості всіх нулів у запису цього числа, враховуючи і нуль цілих, взятих із знаком мінус. Для прикладу
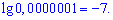
Перейдемо до розгляду практичних завдань. Уважно розгляньте їх розв’язання, це дозволить засвоїти деякі правила логарифмів та збільшить практичну базу, що стане в нагоді при проходженні ЗНО, контрольних і т.д.
Способи розвязування логарифмічних рівнянь:
Приклад 1. Розв’язати рівняння.
Розв’язання. Використовуючи властивість логарифмів переписуємо рівняння у вигляді
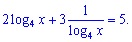
Робимо заміну змінних
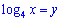
та переписуємо рівняння у вигляді
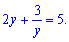
Домножуємо на змінну y та записуємо у вигляді квадратного рівняння
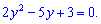
Обчислюємо дискримінант
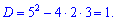
Корені рівняння шукаємо за формулою
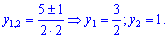
Повертаємося до заміни змінних та знаходимо
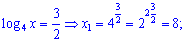
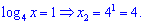
Рівняння має два розв’язки
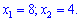
Приклад 2. Розв’язати рівняння.
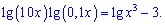
Розв’язання.Розкриваємо дужки та записуємо у вигляді суми логарифмів
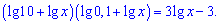
Враховуючи властивості логарифма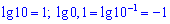 
рівняння перетворимо до вигляду
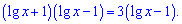
Переносимо доданок за знаком рівності в праву сторону
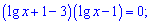
та зводимо до добуту
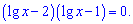
Обидва множники прирівнюємо до нуля та знаходимо невідомі
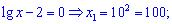
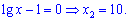
Схема даного завдання досить поширена при обчисленні логарифмічних рівнянь, тому постарайтеся її завчити.
