математика гр.18Т1

Урок 56. Тема: Перпендикуляр і похила.

В підручнику п.35 на стр.185 опрацювати, виписати поняття: ортогональна проекція, перпендикуляр, основа перпендикуляра, похила, основа похилої, проекція похилої, перемалювати рисунки 35.1, 35.2, 35.3, переписати теорему 35.1, задачу № 1 на стр.186. Розв’язати  на стр.190 № 35.3, 35.4, 35.5

Урок 57. Тема: Ортогональне проектування.

Все, що тут записано потрібно уважно прочитати, записати у зошит все що виділене курсивом і усі малюнки:

Для зображення просторових фігур у стереометрії користуються па­ралельним проектуванням. Пригадаємо, що це таке.

Нехай дано довільну площину α, точку А (рис. 83) і пряму h, яке перетинає площину α. Проведемо через точку А пряму, яка паралель­на h, вона перетинає площину α у деякій точці А1. Знайдену таким способом точку А; називають паралельною проекцією точки А на площину α у напря­мі h. Пряму h називають проектуючою пря­мою, площину α — площиною проекцій.

Щоб побудувати проекцію будь-якої фігу­ри, треба спроектувати на площину проекції кожну точку даної фігури (рис. 84). Наведемо деякі властивості паралельного проектування.

Теорема.

Якщо відрізки, які проектуються, не паралельні проектуючій прямій, то при паралельному проектуванні:

1)  відрізки зображаються відрізками;

2)  паралельні відрізки зображаються паралельними відрізками або відрізками однієї прямої;

3) відношення довжин паралельних відрізків і відрізків однієї прямої зберігається.

Доведення

1)  Усі прямі, що проектують точки від­різка АВ, лежать в одній площині β, яка перетинає площину α по прямій А1В1 (рис. 85). Отже, проекцією відріз­ка є відрізок, причому довільна точка С відрізка АВ зображається точкою С1 відрізка А1В1.

2)  Нехай відрізки АВ і CD, які проектуються, паралельні. Усі пря­мі, що їх перетинають і паралельні h, заповнюють або частини од­нієї площини (рис. 86), або паралельних площин (рис. 87).

Ці частини площин перетинають площину а відповідно або по від­різках однієї прямої, або по паралельних відрізках А1В1 і С1D1.

3)  Якщо відрізки АВ і СВ, які проектують, розміщені на одній прямій (див. рис. 85), то за теоремою про пропорційні відрізки має­мо: А1С1 : С1B1 = АС : СВ.

Якщо відрізки АВ і CD паралельні, а їх проекції А1B1 і С1D1 лежать на одній прямій (див, рис. 86), то АВВ2A2 — паралелограм. У цьому випадку A1B1 : C1D1 = A2B2 : CD = AB : CD. Нарешті, якщо проекції А1В1 і С1D1 даних відрізків АВ і CD не лежать на одній прямій (див. рис. 87), то побудуємо паралелограм CDKB. Його проекція — паралелограм СDKВ. Отже, маємо:  А1В1 : C1D1 = А1В1 : В1К1 = АВ : ВК = АВ : CD.

Зображення просторових фігур на площині

Розглянуті властивості паралельного проектування дають змогу на­очно зображати просторові фігури на площині.

Зображенням фігури називається будь-яка фігура, подібна до пара­лельної проекції даної фігури на деяку площину.

Якщо проектуючі прямі перпендикулярні до площини проекцій, таке проектування називають ортогональним, або прямокутним. Ортого­нальне проектування – вид паралельного проектування, тому воно має властивості паралельного проектування. У геометрії ортогональне проек­тування основне. Далі, говорячи про проектування і проекції, ми мати­мемо на увазі тільки ортогональне проектування, ортогональні проекції.

Ортогональне проектування широко застосовується в технічному кресленні.

• • Вивчаючи стереометрію, ми зіткнулися з проблемою зображення просторових фігур на площині. З давніх давен це питання хвилювало не лише математиків, а й художників, конструкторів, архітекторів. Вихід із ситуації підказала сама природа, адже таке явище як тінь – це не що інше, як приклад зображення просторових об’єктів на площині. Пучок променів світла, потрапляючи на об’єкт, відтворює на площині його обриси.

  У математиці цей процес називається проектуванням. 

  Метод центрального проектування дає наочне зображення, бо саме центральна проекція оточуючих предметів утворюється на сітківці ока. Саме нею користуються художники, називаючи перспективою.

  Для математиків, інженерів та інших фахівців кращим виявилось паралельне проектування, бо воно є простішим у плані виконання зображень і зберігає більше властивостей реальних об’єктів.

  Означення. Ортогональним називається проектування, при якому проектуючі прямі перпендикулярні до площини проектування.

  Таке проектування широко використовується не лише в геометрії, а і в технічному кресленні. Ортогональні проекції фігури на три взаємно перпендикулярні площини дають повне уявлення про неї. 

  Оскільки ортогональне проектування є різновидом паралельного, то воно зберігає і всі його властивості, зокрема точки зображаються точками, відрізки – відрізками або точками, прямі – прямими або точками. Довжини відрізків, як відомо, не зберігаються, а як саме вони можуть змінюватися? Чому? пояснення може ґрунтуватися на наслідку з теореми Піфагора, яка, до речі, на мові ортогонального проектування може бути перефразована так: «Квадрат довжини будь-якого відрізка дорівнює сумі квадратів його ортогональних проекцій на 2 взаємно перпендикулярні прямі». 

  Аналогічне твердження правильне і для простору, воно називається просторовою теоремою Піфагора і може бути сформульоване так: «Квадрат довжини будь-якого відрізка дорівнює сумі квадратів довжин його проекцій на три взаємно перпендикулярні прямі».

  Давайте з’ясуємо, як саме залежить площа ортогональної проекції многокутника від кута між площиною многокутника та площиною проекції.

  Теорема: Площа ортогональної проекції многокутника на площину дорівнює добутку його площі  на косинус кута між  площиною многокутника та площиною проекції.

   Урок 58

• Тема: Теорема про три перпендикуляра. Відстань від точки до прямої.
• З підручника на стр. 188 виписати теорему 35.2 з доведенням, переписати задачу 4
• Переглянути презентацію, для цього скопіюйте цю ссилку і забийте її в Googl
• урок 58
• file:///C:/Users/Admin/Desktop/%D1%83%D1%80%D0%BE%D0%BA%2058.pdf
• Урок 59
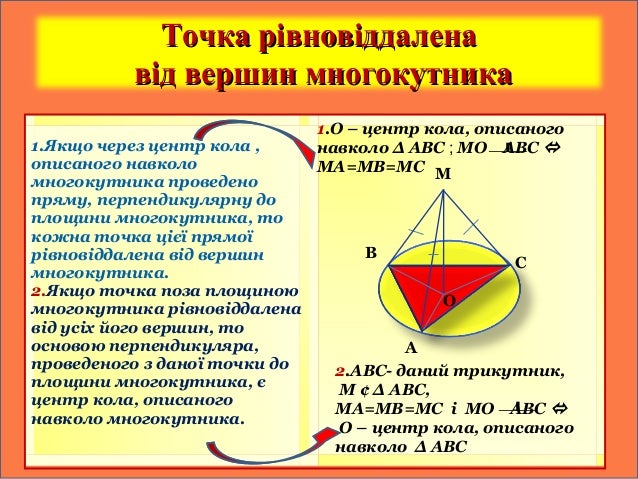
• Тема: Властивості точки рівновіддаленої від сторін многокутника
• Запишіть собі все, що бачите на цих двох картинках, на стр. 191 в підручнику розв’язати задачі № 35.18
• 
•