ФЕДОРІВСЬКИЙ ЦЕНТР ПО Міністерство освіти і науки України
1. Відеоурок
2. Теоретичний матеріал.
В прямокутній системі координат у просторі кожній точці М простору ставиться у відповідність єдина впорядкована трійка чисел, а кожній впорядкованій трійці чисел – єдина точка простору. Цю трійку чисел називають координатами точки. Визначаються вони аналогічно координатам точки на площині.
Проведемо через точку М площину, перпендикулярну до осі х (мал. 516). Вона перетинає вісь х в точці Мx. Координатою х точки М (абсцисою точки М) називають число, яке дорівнює за абсолютною величиною довжині відрізка ОМx; додатне, якщо точка Мх лежить на додатній півосі х і від’ємне, якщо вона лежить на від’ємній півосі. Якщо ж точка М збігається з точкою О, то вважаємо, що абсциса точки М дорівнює О.
Проведемо площини, перпендикулярні осям у і z, які перетинають ці вісі в точках Мy і Мzвідповідно. Аналогічно до координати х точки М визначаються координата у точки М (ординати точки М) і координата z точки М (апліката точки М).
Особливості розташування точок у просторі.
Якщо точка належить осі координат або координатній площині, то деякі її координати дорівнюють нулю. Обернене твердження також вірне: якщо деякі координати точки дорівнюють нулю, то вона належить осі координат або координатній площині.
Наступна таблиця подає залежить між рівністю нулю деяких координат точки і особливістю її розташування.
| Які з координат точки А(х; у; z) дорівнюють нулю | Координати точки | Особливості розташування точки |
| у і z | А(х; 0; 0) | Належить осі х |
| х і z | А(0; у; 0) | Належить осі у |
| x і у | А(0; 0; z) | Належить осі z |
| z | А(х; у; 0) | Належить площині ху |
| y | А(х; 0; z) | Належить площині хz |
| x | А(0; у; z) | Належить площині уz |
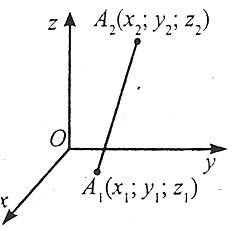
Відстань між двома точками
Відстань між двома точками дорівнює квадратному кореню із суми квадратів різниць однойменних координат.
Відстань між двома точками в просторі
,
де d – відстань між точкою А1 із координатами (х1;у1;z1) і точкою А2 із координатами (х2;у2;z2).
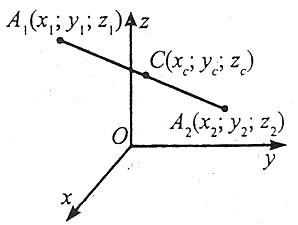
Координати середини відрізка
Координати середини відрізка дорівнюють півсумі відповідних координат його кінців.
Координати середини відрізка на площині
Координати (хс;ус;zc) точки С, що є серединою відрізка, визначаються за формулами
,
де (х1;у1;z1) і (х2;у2;z2) – координати точок А1 і А2, що є кінцями відрізка.
Рівняння фігури
Рівнянням фігури в декартових координатах у просторі називається рівняння із трьома невідомими х, у, z, які задовольняють координати будь-якої точки фігури, і тільки вони.
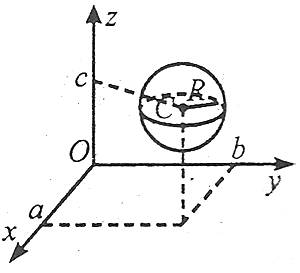
Рівняння сфери
Якщо в просторі задано деяку точку з координатами С(а,b,c), що є центром сфери, а також радіус R, то рівняння сфери має вигляд
.
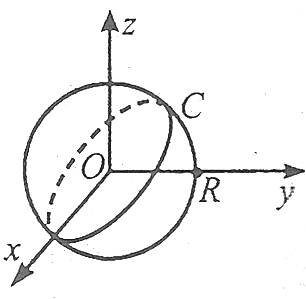
Якщо центром сфери є початок координат, то маємо
.
Перетворення фігур на площині
Симетрія
|
Точки Симетрія відносно |
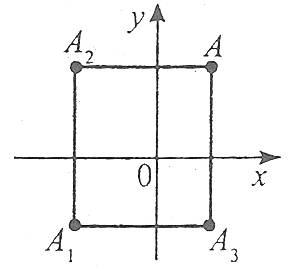
А(1;1) |
А(х;у) |
|
точки О |
А1(-1;-1) |
А1(-х;-у) |
|
осі х |
А3(1;-1) |
А3(х;-у) |
|
осі у |
А2(-1;1) |
А2(-х;у) |
Паралельне перенесення
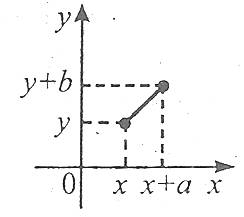
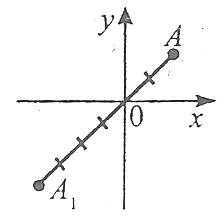
Гомотетія відносно точки О
3. Розвязування задач.
Приклад 1. Задано точки А(1;2;3), В(0;1;2), С(1;0;0), D(1;0;2). Які з цих точок лежать: 1) у площині XOZ; 2) на осі ОХ; 3) у площині YOZ?
Розв’язання
- Якщо точка лежить у площині XOZ, то координата у дорівнює 0, у площині XOZ лежать точки С(1;0;0), D(1;0;2).
- Якщо точка лежить на осі ОХ, то координата у і z дорівнюють нулю, отже, на осі ОХ лежить точка С(1;0;0).
- У площині YOZ лежить точка В(0;1;2).
Відповідь: 1) С, D; 2) С; 3) В.
Приклад 2. Задано точки А(1;2;3), В(2;3;1), С(3;1;2). Знайдіть периметр трикутника АВС.
Розв’язання
Оскільки
,
,
,
то 
.
Відповідь: 
.
Приклад 3. Знайдіть координати точки С – середини відрізка АВ, якщо А(1;2;3), В(-3;2;1).
Розв’язання
Оскільки А(1;2;3), В(-3;2;1) і АС=СВ, то
.
Отже, С(-1;2;2).
Відповідь: С(-1;2;2).
Приклад 4. Складіть рівняння сфери з центром в точці В(1;1;3), якщо відомо, що сфера проходить через точку М(2;0;-1).
Розв’язання
Знайдемо радіус R сфери
.
Ураховуючи, що центр сфери міститься в точці В(1;1;3), а радіус R сфери дорівнює 
, матимемо рівняння сфери
.
Відповідь: 
.
