ФЕДОРІВСЬКИЙ ЦЕНТР ПО Міністерство освіти і науки України
1) Опорний конспект до уроку для учнів. Повторення навчального матеріалу
Вступ до стереометрії
Стереометрія – розділ геометрії, що вивчає фігури в просторі
Основні фігури в просторі: точка, пряма , площина
Аксіоми стереометрії:
Аксіома 1. Яка б не була площина, існують точки, що належать цій площині, і точки, які не належать їй
Аксіома 2. Якщо дві різні прямі мають спільну точку, то через них можна провести площину і до того ж тільки одну
Аксіома 3. Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку
Наслідки з аксіом стереометрії:
1) Через три точки, що не лежать на одній прямій можна провести площину і до того ж тільки одну;
2) Через пряму і точку, що не належить їй, можна провести площину і до того ж тільки одну;
3) Якщо дві точки прямої на лежать площині, то і вся пряма належить цій площині.
Перерізи
- Якщо принаймні дві точки просторової фігури лежать по різні боки від площини, то говорять, що площина цю фігуру перетинає. А площину називають січною.
- Перерізом многогранника називається фігура, яка складається з усіх точок, які є спільними для многогранника і січної площини
- Вид перерізу залежить від розміщення площини
- кількість сторін многокутника перерізу не може перевищувати кількості граней даного многогранника
Площину перерізу можна задати:
1. Трьома точками, що не лежать на одній прямій;
2. Прямою і точкою, що не лежить на ній;
3. Двома прямими, що перетинаються;
4. Двома паралельними прямими;
Побудувати переріз многогранника площиною – означає:
ü в площині кожної перетнутої грані вказати дві точки, що належать перерізу;
ü з’єднати ці точки прямою;
ü знайти точки перетину прямої з ребрами многогранника.
Метод слідів:
Якщо площина α перетинає площину β по прямій а, то пряму а називають слідом площини α на площину β.
Метод слідів включає три важливих пункти:
v Будується лінія перетину (слід) січної площини з площиною основи многогранника.
v знаходимо точки перетину січної площини з ребром многогранника.
v Будуємо і заштриховуємо переріз.
Паралельність прямої і площини
Дві прямі у просторі називаються паралельними, якщо вони лежать в одній площині та не перетинаються.
Наприклад: а та b паралельні. Паралельність прямих а та b позначається так: 
.
Теорема про існування єдиної прямої, паралельної даній прямій
Через точку, яка не лежить на прямій, можна провести пряму, паралельну цій прямій, до того ж тільки одну.
Ознака паралельності прямих
Дві прямі, паралельній третій прямій, паралельні, якщо 
, то 
.
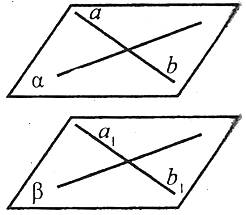
Дві прямі називають мимобіжними, якщо вони не лежать в одній площині.
Наприклад: а і b мимобіжні.
Ознака мимобіжності прямих
Якщо одна із двох прямих лежить у деякій площині, а друга пряма перетинає цю площину в точці, яка не лежить на першій прямій, то ці прямі мимобіжні.
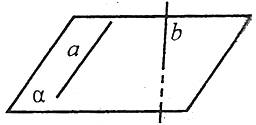
Пряма та площина називаються паралельними,якщо вони не мають спільних точок.
Наприклад: пряма а та площина α паралельні. Паралельність прямої а та площини α позначається так: 
.
Ознака паралельності прямої та площини
Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині. Якщо 
.
3. Паралельні площини і площини, що перетинаються
Якщо дві різні площини мають спільну точку, то вони перетинаються.
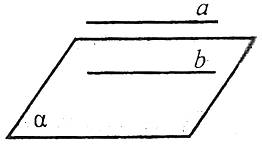
Дві площини називаються паралельними, якщо вони не перетинаються.
Наприклад: площини α та β паралельні. Паралельність площин α та β позначається так: 
.
Ознака паралельності площин
Дві прямі, що перетинаються, однієї площини паралельні відповідно двом прямим другої площини, то ці площини паралельні.
Наприклад: Якщо 
, то 
.
Існування єдиної площини, паралельної даній площині
Через точку, яка не належить даній площині, можна провести площину, паралельну даній, і до того ж тільки одну.
Властивості паралельних площин
1. Якщо дві паралельні площини перетинаються третьою, то прямі перетину паралельні.
Наприклад: 
, γ перетинає α по прямій а, γ перетинає β по прямій b, тоді 
.
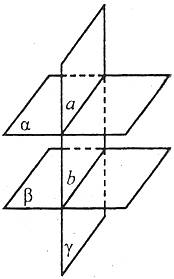
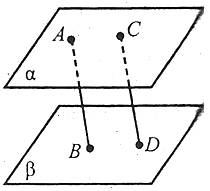
2. Відрізки паралельних прямих, які розташовані між паралельними площинами, рівні.
Наприклад: 
, отже, АВ=CD.
2. Розвязування типових задач
3.Домашнє завдання.
Повторити весь теоретичний матеріал. Підготуватись до контрольного тестування з теми “Вступ у стереометрію. Паралельність прямих і площин в просторі”
Нагадую тематичне тестування буде доступне лише тим, хто виконав попередні уроки.
Виконати письмово №4.16-4.17
