1.Повторення раніше вивченого матеріалу
Степенем (степінь – power) називається добуток кількох рівних множників:
Наприклад
2·2·2=23;
7·7·7·7·7·7=76.
Розглянемо степінь
45
Число 4 називається основою степеня (основа степеня – base of power). Число 5 називається показником степеня (показник степеня – exponent).
Вираз читається так:
чотири у п’ятому степені.
Спеціальні назви степеня:
a2 читається: a в квадраті або квадрат a;
a3 читається: a в кубі або куб a.
Наприклад
23 – два в кубі;
52 – п’ять в квадраті.
Порядок дій при обчисленнях
Додавання і віднімання вважаються діями першого ступеня, мно-ження і ділення – другого ступеня, піднесення до степеня – дія третього ступеня. Обчислюючи значення виразу, спочатку виконують дії вищого ступеня, потім – нижчого. Дії одного й того самого ступеня виконуються в тому порядку, в якому вони записані. Якщо вираз містить дужки, спочатку знаходять значення виразу в дужках.
Властивості степенів
Для будь-яких x, y і додатних a і b справедливі рівності:
a·a·a·…·a=ax; a0=1; a1=a;
ax·ay=ax+y; ax:ay=ax-y;
(ax)y=axy; (ab)x=axbx;
(a/b)x=ax/bx; a-x=1/ax.
Степінь дійсного числа з натуральним показником. Його властивості
Нехай ![]() .
. ![]() – це степінь, а – основа степеня, п – показник степеня. Степінь
– це степінь, а – основа степеня, п – показник степеня. Степінь ![]() є добутком п множників, кожний з яких дорівнює а:
є добутком п множників, кожний з яких дорівнює а: 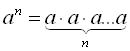 .
.
Будь-який степінь додатного числа є додатним числом, наприклад: ![]()
![]()
![]()
![]() . Парний степінь від’ємного числа є додатним числом, наприклад:
. Парний степінь від’ємного числа є додатним числом, наприклад: ![]()
![]()
![]()
![]() . Непарний степінь від’ємного числа є числом від’ємним, наприклад:
. Непарний степінь від’ємного числа є числом від’ємним, наприклад: ![]()
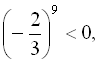
![]()
Нехай ![]()
![]()
![]()
![]() Тоді справедливі такі властивості степеня з натуральним показником:
Тоді справедливі такі властивості степеня з натуральним показником:
1) ![]() ; 2)
; 2) 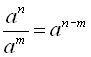 ;
;
3) ![]() ; 4)
; 4) ![]() ;
;
5) 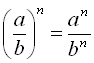 ; 6)
; 6) ![]() ; 7)
; 7) ![]() .
.
Приклад 1: Обчислити вираз 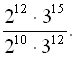
Розв’язання
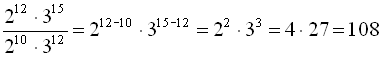 .
.
Відповідь: ![]() .
.
Степінь дійсного числа з нульовим і від’ємним цілим показником
Нехай ![]()
![]() . Припустимо за визначенням
. Припустимо за визначенням ![]()
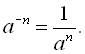
Властивості 1) – 6) степеня з натуральним показником справедливі і для степеня дійсного числа з від’ємним цілим показником. Наприклад: 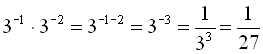 .
.
Степінь з дробовим показником
Якщо ![]() і
і ![]() – натуральні числа,
– натуральні числа, ![]() , то
, то ![]() ; якщо
; якщо ![]() . То
. То 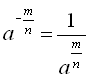 .
.
Нецілий степінь від’ємного числа не має змісту.
Степінь дійсного числа з дійсним показником має ті ж властивості, що і степінь з натуральним і цілим показником. Запишемо ці властивості, припускаючи, що ![]()
1) ![]() ; 2)
; 2) 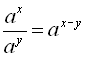 ;
;
3) ![]() ; 4)
; 4) ![]() ;
;
5) 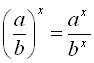 ; 6)
; 6) 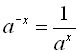 ;
;
7) ![]() ; 8)
; 8) ![]() ;
;
9) ![]() .
.
2. Вивчення нового матеріалу
Завдання. Записати у зошит конспект уроку, виконати відповідні малюнки


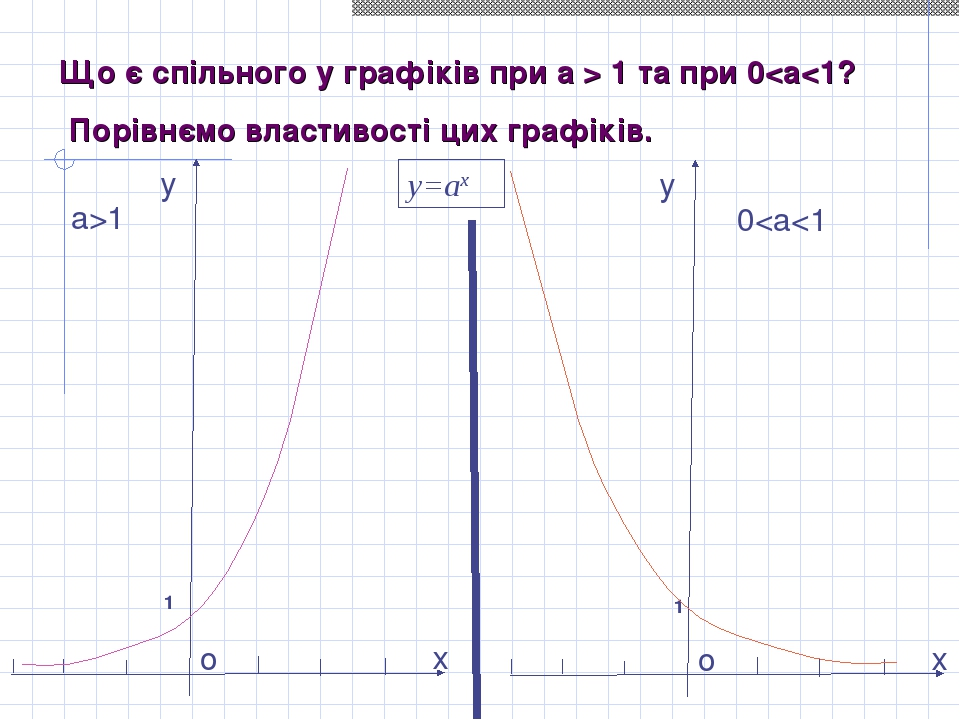
Опрацювати приклади розвязання завдань, зробити записи в зошит


 ФЕДОРІВСЬКИЙ ЦЕНТР ПО Міністерство освіти і науки України
ФЕДОРІВСЬКИЙ ЦЕНТР ПО Міністерство освіти і науки України
