ФЕДОРІВСЬКИЙ ЦЕНТР ПО Міністерство освіти і науки України
Вам нужно сначала закончить Паралельність прямої і площини. Урок №2 для перехода к этому уроку
Опрацювання нового матеріалу.
Ми знаємо, якщо дві різні площини мають спільну точку, то вони перетинаються по прямій (аксіома С2). Звідси випливає, що дві площини або перетинаються по прямій, або не перетинаються, тобто не мають спільних точок (демонструємо схему, наведену нижче).
Дві площини називаються паралельними, якщо вони не перетинаються.
Ознака паралельності площин.
Якщо дві прямі, що перетинаються, однієї площини відповідно паралельні двом прямим, що перетинаються, другої площини, то ці площини паралельні.
Доведення.
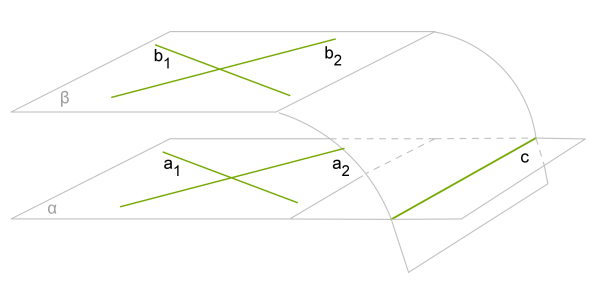
Нехай α і β — дані площини, a1 і a2 — прямі, що перетинаються в площині α, а b1 і b2 відповідно паралельні їм прямі в площині β.
Припустимо, що площини α і β не паралельні, тобто вони перетинаються по деякій прямій c.
Пряма a1 паралельна прямій b1, отже вона паралельна і площині β.
Пряма a2 паралельна прямій b2, отже, вона паралельна і площині β (ознака паралельності прямої і площини).
Пряма c лежить у площині α, отже принаймні одна з прямих a1 або a2 перетинає пряму c, тобто має з нею спільну точку. Але пряма c також лежить і в площині β, це означає, що перетинаючи пряму c, пряма a1 або a2 перетинає площину β, чого бути не може, так как прямі a1 і a2 паралельні площині β.
Таким чином, площини α і β не перетинаються, тобто вони паралельні.
Закріплення нового матеріалу.
