Не пропусти
Головна / Урок / Паралельність площин. Властивості паралельних площин( урок №2)

Паралельність площин. Властивості паралельних площин( урок №2)

Вам нужно сначала закончить Паралельність площин для перехода к этому уроку
1. Опрацювання нового матеріалу.

Переглянути відеоурок. Записати властивості паралельних прямих, зробити відповідні малюнки

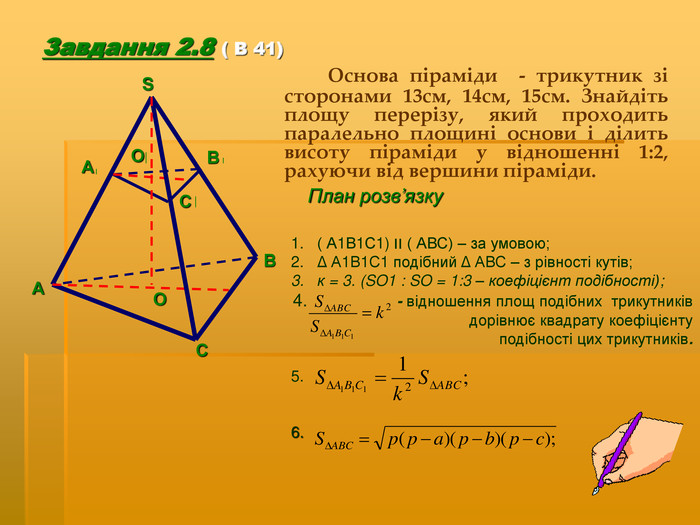
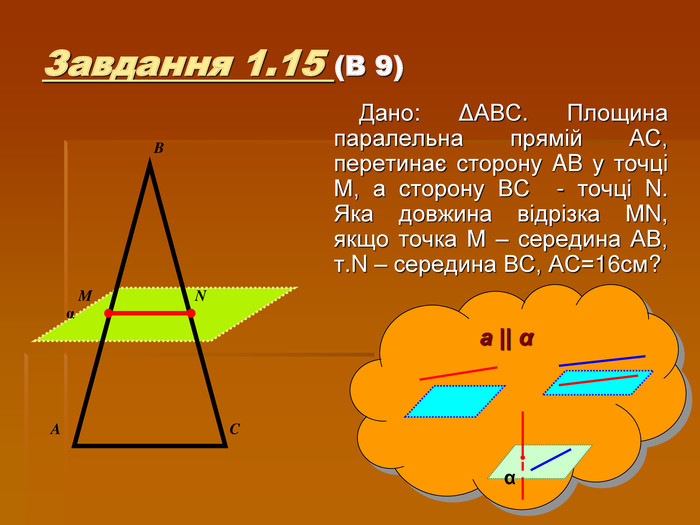
2.Закріплення нового матеріалу

( А1В1С1) ׀׀ ( АВС) – за умовою; Δ А1В1С1 подібний Δ АВС – з рівності кутів; к = 3. (SO1 : SO = 1:3 – коефіцієнт подібності); - відношення площ подібних трикутників дорівнює квадрату коефіцієнту подібності цих трикутників. 5. 6. Завдання 2.8 ( В 41) Основа піраміди - трикутник зі сторонами 13см, 14см, 15см. Знайдіть площу перерізу, який проходить паралельно площині основи і ділить висоту піраміди у відношенні 1:2, рахуючи від вершини піраміди. План розв’язку А В С О А В С О S

Завдання 2.8 ( В 75) Паралельно осі циліндра, радіус основи якого дорівнює 6√2см проведено площину, що перетинає основу циліндра по хорді, яка стягує дугу, градусна міра якої дорівнює 90є. Знайдіть площу перерізу, якщо кут між діагоналлю перерізу і вказаною хордою дорівнює 60є. План розв’язку ОО1 – відрізок вісі циліндра. (АВС) ׀׀ ОО1 – за умовою. АВ׀׀ОО1; СD׀׀ОО1 АВСD – прямокутник; АD –хорда, яка стягує - прямокутний. АО = ОD = R = 6√2см. ΔACD: SABCD = AD • DC.

3.Домашнє завдання.

Завдання 1.15 (В 9) α N M B C A а || α α Дано: ΔАВС. Площина паралельна прямій АС, перетинає сторону AB у точці М, а сторону ВС - точці N. Яка довжина відрізка МN, якщо точка М – середина АВ, т.N – середина ВС, АС=16см?

Вернуться к: група №95 Вступ в стереометрію. Паралельність прямих і площин в просторі.
Всі права захищено © 2025 ФЕДОРІВСЬКИЙ ЦЕНТР ПРОФЕСІЙНОЇ ОСВІТИ | При використанні матеріалів гіперпосилання на ресурс обов'язкове
x

Перегляньте також

2365498561521

Створюємо власний освітній контент

19 травня 2025 року у Федорівському центрі професійної освіти відбулося чергове засідання ...