Дистанційний курс Олени Малахової

Завдання для групи 16Т3 з предмету «Математика»

Афанасьєва О.М., Бродський Я.С., Павлов О.Л. «Математика. 11 клас: Підручник для загальноосвітніх навчальних закладів. Рівень стандарту. – Тернопіль, 2012. – 480с.

19.03.2020

Урок 55

Тема: Графічне подання інформації про вибірку.

Презентація

https://www.youtube.com/watch?v=h2EjoMZBEgg

Законспектувати

Вибіркові характеристики. Графічне подання інформації про вибірку

У математичній статистиці замість слова“дані”використовується термін“варіанти”. Числову характеристику варіанти при цьому називаютьознакою.Варіанти, що записані в таблиці за зростаючим (спадаючим) порядком, називаютьваріаційним рядом. Варіаційні ряди бувають дискретними та інтегральними.

Таблиця яка встановлює зв’язок між рядом варіант і відповідними частотами називається частотною (таблицею), або статистичним розподілом.Тут N – обсяг вибірки: N=n₁+n₂+…+n_m.

*х_і*	х₁	х₂	...	*x_m*
*n_i*	n₁	n₂	*. . .*	*n_m*

Перейти від частот до відносних частот у такому розподілі вибірки обсягом N = 20.

*Варіанта х_і*	2	6	12	*Розв’язання*Знайдемо відносні частоти: ; ; .
*Частота* *n_i*	3	10	7	*Розв’язання*Знайдемо відносні частоти: ; ; .
Тому одержимо такий розподіл:				*Варіанта х_і*	2	6	12
Тому одержимо такий розподіл:				*Відносна частота р*_i	0,15	0,50	0,35

Для графічного зображення статистичного розподілу використовуються полігони і гістограми.

Полігон частот це ламана лінія, відрізки якої сполучають точки з координатами (x_i;n_i) .
Аггоритм побудови полігону частот:
на осі абсцис відкласти варіанти x_i, далі на осі ординат – відповідні їм частоти n_iта з’єднати їх.

Полігоном відносних частот це ламана пряма, що сполучає точки з відповідними координатами (x_i;v_i)
Побудова полігона відносних частот полягає в послідовному з’єднанні варіант x_iв осях (x_i;v_i).

Для побудови полігона на осі ОХ відкладають значення варіант х_і, на осі ординат – значення частот n_i. Точки (х_і; n_i) з’єднують відрізками прямих і одержують полігон частот.

Гістограмою частот називають східчасту фігуру, яка складається з прямокутників, основами яких є інтервали довжиною h, а висота дорівнює відношенню .

Площа і-го прямокутника дорівнює

Отже, площа гістограми дорівнює сумі всіх частот, тобто обсягу вибірки.

Гістограма частотцеступінчаста (східчаста) фігуру,яка має вигляд сполучених прямокутників, основа яких рівна інтервалам довжиною h, а висоти рівні відношенню n_i/h (густина частоти).

Гістограма відносних частот це ступінчаста фігура, подібна до гістограми частот, тільки по осі ординат відкладені густина відносних частот p_i/h.

Завдання для групи 16Т3 з предмету «Економіка»

Економіка (рівень стандарту, академічний рівень), 11 клас, І.Ф. Радіонова. – Камянець-Подільський: Аксіома, 2011. – 176 с.

Урок 26.(19.03.2020)

Тема: Сучасне світове господарство. Міжнародні економічні відносини.

Стр.136-142, опрацювати, виписати основні поняття.

Урок 27 (26.03.20)

Тема. Міжнародні організації валютного регулювання, Валютні курси та умови зовнішньої торгівлі.

Стр. 139-149, опрацювати, виписати основні поняття.

Розділ 4. Тема 9. Міжнародна торгівля, валютні відносини, рух капіталів між країнами, п.9.1, 9.2 на стр.136 – 142 опрацювати. Виписати поняття, які виділені чорним шрифтом на цих сторінках.

Завдання для групи 17Т2 з предмету «Математика»

17.03.2020

Урок 55

Тема: Інтеграл та його застосування. Первісна та її властивості.

Відкрити цю зноску, виписати правила, таблицю, формули.

https://mathab.com.ua/pochatki-analizu/pervisna-integral/pervisna-ta-%D1%97%D1%97-vlastivosti-neviznachenij-integral.html

або

На ст.. 206 §9 п.1, опрацювати увесь пункт, виписати поняття «інтегрування», «первісна», основну властивість первісної, записати таблицю первісних на стр.209.

Урок 56

Тема: Таблиця первісних.

Відкрити цю зноску, виписати правила, таблицю, формули.

https://mathab.com.ua/pochatki-analizu/pervisna-integral/pervisna-ta-%D1%97%D1%97-vlastivosti-neviznachenij-integral.html

На ст.. 211 §9 п.2, опрацювати увесь пункт, виписати три властивості первісних, записати приклади на стр. 212, 213, 214. Розібратися з таблицею первісних зі стр.209, вивчити її напам’ять.

19.03.2020

Урок 57

Тема: Розв’язування вправ.

Відкрити цю зноску, виписати правила, таблицю, формули.

https://mathab.com.ua/pochatki-analizu/pervisna-integral/pervisna-ta-%D1%97%D1%97-vlastivosti-neviznachenij-integral.html

https://studfile.net/preview/5751453/page:8/

На стр.215 виконати вправи №№176, 183 (1-5)

24.03.2020

Урок 58

Тема: Розв’язування вправ.

приклади

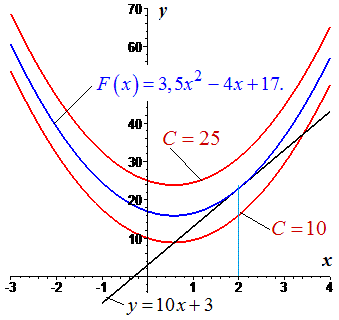
Приклад 217. Знайдіть первісну функції 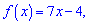для графіка якої пряма y=10x+3 є дотичною.

Розв’язання:
Досить цікаве завдання. Обчислюємо первісну
первісна функції
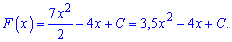
Пряма дотикається до графіка означає, що первісна рівна дотичній лише в одній точці. Це можливо, якщо дискримінант квадратного рівняння рівний нулю
умова
квадратне рівняння
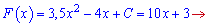
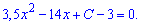
Знаходимо невідому з умови

обчислення сталої

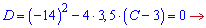
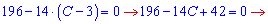
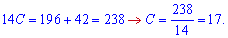
Шукане рівняння первісної матиме вигляд

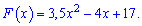
Графік первісних та дотичної наведено нижче
графік первісної

Приклад 218. Швидкість руху точки задається рівнянням 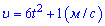. Знайдіть рівняння руху S=S(t) якщо у момент часу t = 3 с точка знаходилася на відстані S = 42 м.

Розв’язання:
Рівняння руху знаходимо через первісну від швидкості
шлях
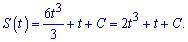
З умови, що в початковий момент часу S(t)=42 знаходимо невідому сталу
42=2*27+3+С; 42=57+С;
С=42-57=-15.
Підставляємо отримане значення в рівняння руху

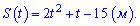
Приклад 219. Знайдіть загальний вигляд первісних функції:

1) функція
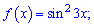
Розв’язання:
В цьому прикладі і наступних потрібно понизити степінь або звести до спільної основи, якщо задано тригонометричні функції. Представимо функцію у вигляді
перетворення
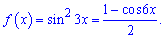
За таблицею первісну знаходимо без проблем
первісна функції

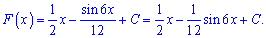
2) функція
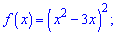
Розв’язання:
Піднімаємо вираз у дужках до квадрату
піднесення до квадрату
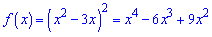
та застосовуємо первісну
первісна функції

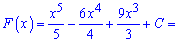
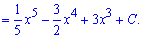
3) функція
Розв’язання:
Добуток синусів представимо у вигляді суми
перетворення синусів

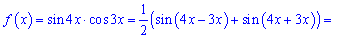
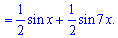
Тоді первісну знаходимо з таблиці
первісна функції

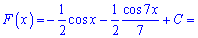
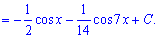
24.03.2020

Урок 59

Тема: Обчислення первісних, що задовольняють задані початкові умови.

Завдання №1 Знайти первісну функції f(x)=3×2-6x+2, графік якої проходить через точку А(-1;5).

Це завдання складається з двох частин:

1) знайти первісну;
2) у знайдену первісну підставити х = -1 і F(x)=5 та знайти значення С.
F(x)=

Оскільки графік отриманої первісної проходить через точку

А(-1;5), то підставимо замість х число (-1), а замість

F(x) – число 5.

Отримаємо:

5=(-1)3-3(-1)2+2(-1)+С;

5= -6+С;

С=11.

Відповідь: F(x)=x3-3×2+2x+11.

Завдання №2.Знайти первісну для функції,

а)f(x) = 5 sin x – x3; б) f(x)= ;

в) f(x) = .

графік якої проходить через точку А( 1; 8).

Самостійна робота

1. Знайти первісну для функції:

а)f(x) = 3 cos x – x3 ; б) f(x) = ; в) f(x) =

2. Знайти для функції первісну, графік якої проходить через точку А( -1; 0).

Домашнє завдання

АфанасьєваО.М.,БродськийЯ.С.,ПавловО.Л.,СліпенкоА.К.Математика.11клас:
Підручник для загальноосвітніх навчальних закладів. Рівень стандарту. – Тернопіль: Навчальна книга – Богдан, 2011.
Опрацювати за підручником с.212 (приклад 3), розв’язати задачі 1780, 190*.

26.03.2020

Урок 60

Тема: Розв’язування вправ

За цією зноскою виписати усі приклади, розібратися з розв’язками.

https://studfile.net/preview/5751453/page:8/

Завдання для групи 18Т1 з предмету «Математика»

А.Г.Мерзляк, Д.А.Номіровський, В.Б.Полонський, М.С.Якір «Математика.Алгебра і початки аналізу та геометрія. Рівень стандарту Підручник 10 клас для загальноосвітніх навчальних закладів. . – Х: Гімназія, 2018. – 256с.

18.03.2020

Урок 46

Тема: Розв’язання найпростіших тригонометричних рівнянь способом розкладання на множники.

Відкрити цю зноску, опрацювати конспект, виписати правила та приклади.

https://fizmat.7mile.net/algebra-10/24-trig-rivniannia-rozkladanya-na-mnozhniki.htm

На стр. 95 розв’язати рівняння №№16.12, 16.10

Урок 47

Тема: Розв’язання найпростіших тригонометричних рівнянь за допомогою тригонометричних формул.

На стр.95 розв’язати №№ 16.6, 16.4, 16.2

20.03.2020

Урок 48

Тема: Розв’язання тригонометричних рівнянь, які зводяться до квадратних.