Урок 77

Тема: Конус, його елементи.

Перемалюйте усі малюнки з позначеннями, розв’яжіть кросворд

Теорія:

Конус — тіло обертання, яке виходить в результаті обертання прямокутного трикутника навколо його катета.

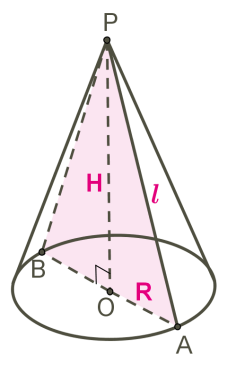
Трикутник POA обертається навколо сторони PO.
PO — вісь конуса і висота конуса.
P — вершина конуса.
PA — твірна конуса.
Коло з центром O – основа конуса.
AO — радіус основи конуса.
Осьовий переріз конуса — це переріз конуса площиною, яка проходить через вісь PO конуса.
Осьовий переріз конуса — це трикутник.
APB — осьовий переріз конуса.

∡PAO=∡PBO — кути між похідними і основою конуса.

Розгорткою бічної поверхні конуса є круговий сектор. Довжина дуги сектора — це довжина кола основи конуса довжиною 2πR, кут розгортки бічної поверхні α.

В конусі не можна позначити кут розгортки.
На розгортці конуса не можна позначити висоту і радіус конуса.

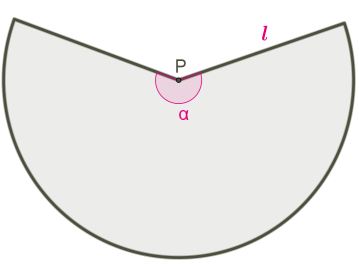
Радіус сектора — це твірна конуса.

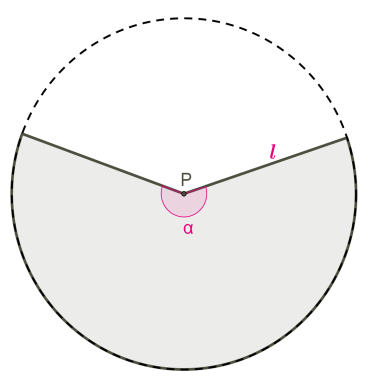
Таким чином, бічна поверхня конуса є частиною повного кола з радіусом l:

Sбіч.=πl2⋅α360°

Довжина дуги також є частиною довжини повного кола з радіусом l, але у той же час довжина дуги – це довжина кола основи конуса з радіусом R.
Порівняємо вирази довжини дуги і виразимо α через R:

2πl⋅α360°=2πRα=2πR⋅360°2πl=R⋅360°l

Отримуємо ще одну формулу бічної поверхні конуса, не використовується кут розгортки бічної поверхні:

Sбіч.=πl2⋅R⋅360°360°⋅l=πRl

Зрізаний конус

Якщо провести переріз конуса площиною, перпендикулярної осі конуса, тоді ця площина розбиває конус на дві частини, одна з яких — конус, а іншу частину називають зрізаним конусом.

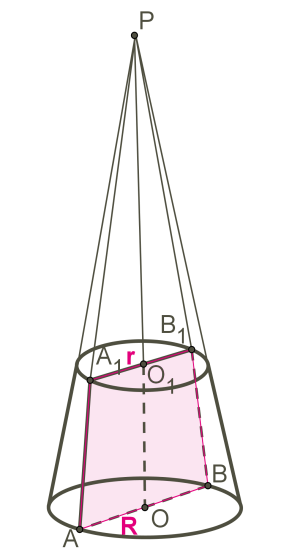
Також, зрізаний конус можна розглядати, як тіло обертання, яке утворилося в результаті обертання прямокутної трапеції навколо бічної сторони (яка перпендикулярна до основи трапеції) або у результаті обертання рівнобедреної трапеції навколо висоти, проведеної через серединні точки основ трапеції.

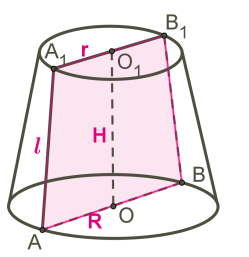
OO1 — вісь конуса і висота конуса.

AA1 — твірна конуса.

Кола з центрами O і O1 — основи зрізаного конуса.

AO і A1O1 — радіуси основ конуса.

Осьовий переріз конуса — це переріз конуса площиною, яка проходить через вісь OO1 конуса.

Осьовий переріз конуса — це рівнобедрена трапеція.

AA1B1B — осьовий переріз конуса.

Бічна поверхня визначається, як різниця бічної поверхні даного конуса і відтятого конуса:

Sбіч.=πR⋅PA−πr⋅PA1=πR⋅(PA1+AA1)−πr⋅PA1==πR⋅PA1+πR⋅AA1−πr⋅PA1==πR⋅l+(πR−πr)⋅PA1

Оскільки ΔPAO∼ΔPA1O1, тоді сторони їх пропорційні:

PAPA1=Rrl+PA1PA1=Rrr⋅(l+PA1)=R⋅PA1rl=R⋅PA1−r⋅PA1PA1⋅(R−r)=rlPA1=rlR−r

Таким чином, отримуємо формулу бічної поверхні зрізаного конуса, яка містить радіуси основ і твірну зрізаного конуса:

Sбіч.=πRl+π⋅PA1⋅(R−r)=πRl+π⋅rlR−r⋅(R−r)Sбіч.=πRl+πrl=πl⋅(R+r)

Урок 78

Тема: Перерізи конуса, осьовий переріз конуса

Відкрийте цю презентацію: 214511, випишіть з неї усю інформацію

Урок 79

Тема: Розвязування задач 

Перепишіть ці задачі з малюнками:

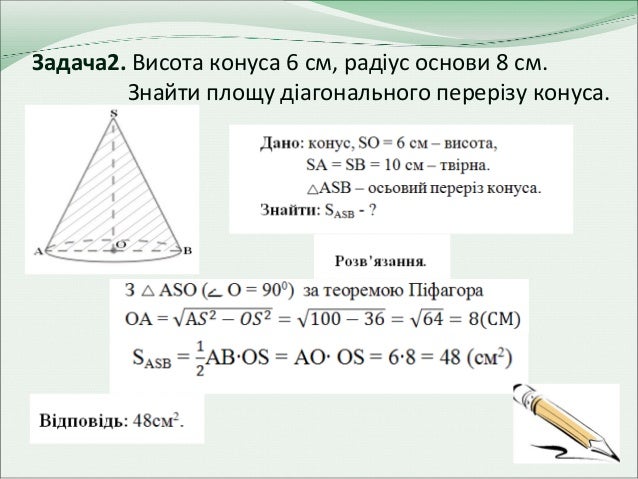
за цією зноскою електронний підручник, відкрийте його

http://kropivnitsky.maup.com.ua/assets/files/11-klas-matematika-merzljak-2019.pdf

і на стр.128 у пункті 20 перечитайте усю теорію, і на стр. 130 розв’яжіть задачі №№ 20.1, 20.2, 20.3, 20.4, 20.5, 20.10, 20.11