Опрацювати розвязки задач, зробити записи в зошит
№1. Площа паралелограма АВСD дорівнює 12. Точка К лежить на прямій СD. Знайдіть площу трикутника АВК.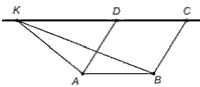

Розв’язання: Невідомо як братися за таку задачу, але вихід є. Поданий малюнок можемо замінити своїм, для збереження геометрії головне дотриматися умови задачі. Побудуємо паралелограм ABCD, далі з вершини B проведемо діагональ паралелограма до точки D.
З точки А до продовження основи проведемо пряму, паралельну діагоналі.
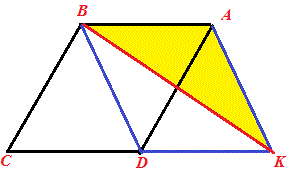 Виконана побудова не суперечить умові задачі. Паралелограми ABCD та ABDK подібні між собою і мають одинакові площі. BK є діагоналлю паралелограма і ділить його на два рівні за площею трикутники. Нам потрібно знайти площу трикутника ABK, для цього розділимо площу паралелограма навпіл
Виконана побудова не суперечить умові задачі. Паралелограми ABCD та ABDK подібні між собою і мають одинакові площі. BK є діагоналлю паралелограма і ділить його на два рівні за площею трикутники. Нам потрібно знайти площу трикутника ABK, для цього розділимо площу паралелограма навпіл
S=12/2=6.
Завжди де це можливо підміняйте складну задачу на побудову простою і зрозумілою Вам. Якщо умова задачі буде дотримана, то це допоможе швидко знайти правильний результат. Особливо це стосується тестування, коли часу обмаль, і немає можливості довго розмірковувати над способами вирішення задач.
Відповідь: Б.
№2. Драбину, довжиною 6,5 м приставили до стіни будинку на рівні вікна (див. рис.). Нижній кінець драбини знаходиться на відстані 2,5 м від будинку. Знайдіть висоту, на якій розташовано вікно.
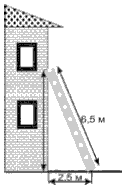

Розв’язання: З побудови бачимо, що драбина виступає в ролі гіпотенузи прямокутного трикутника. Відомий один катет, другий – це шукана висота будинку до вікна.
За теоремою Піфагора обчислюємо
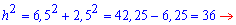
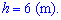
Відповідь: Д.
№3. На папері зображено п’ятикутник АВСDЕ. Відомо, що площа однієї клітинки дорівнює 1 см. Знайдіть площу п’ятикутника.
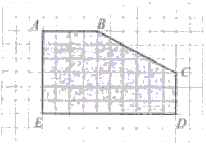

Розв’язання: Найпростіше розбити зображений 5-кутник на два прямокутники і трикутник. Так в геометричних задачах поступайте завжди.
Сторони прямокутника рівні
3,10 та 3,4 сантиметри,
катети прямокутного трикутника – 3, 6 сантиметрів.
Знаходимо площу п’ятикутника
S=3*10+3*4+3*6/2=30+12+9=51 (сантиметр квадратний).
Відповідь: Г.
№4 Через точку О, точку перетину діагоналей квадрата АВСD, проведено перпендикуляр МО до його площини. Відомо, що АD = 8. Знайдіть відстань між прямими АВ
Розв’язання: Для розуміння умови та простоти аналізу виконаємо побудову квадрата та нормалі до нього.
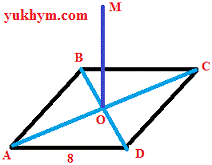
Далі бачимо, що задані прямі між собою мимобіжні. А відстань дорівнює висоті трикутника, побудованого на діагоналях квадрата. Без обчислень відомо, що висота трикутника рівна половині сторони квадрата. Тобто відстань від сторони квадрата до перпендикуляра, що проходить через його центр рівна AD/2=8/2=4. В 10 класі таку побудову і обчисленні повинні вміти виконати усі школярі.
Це відповідає варіанту Г тестів.
Відповідь: Г.
Домашнэ завдання:
№1.Обчисліть довжину меншої діагоналі прямої призми, в основі якої ромб із стороною 6 м та гострим кутом 60°. Висота призми 8 м.
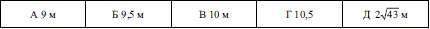
№2. Задано точку А(-1; 2; 3). Укажіть координати точки, симетричної точці А відносно площини ху.
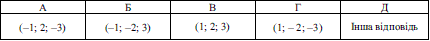
№3. Дано точку Р(-1;3;5). Знайдіть координати точки Q, симетричної точці Р відносно координатної площини уz.
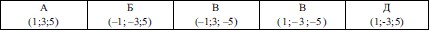
 ФЕДОРІВСЬКИЙ ЦЕНТР ПО Міністерство освіти і науки України
ФЕДОРІВСЬКИЙ ЦЕНТР ПО Міністерство освіти і науки України
